Delische Verwandlungen
Norbert Hungerbühler & Michael Nüsken.
Elemente der Mathematik 1 (2006), 1-19.
Vortrag (Powerpoint Pack and Go).
Abstract
Ernst Specker asked in Aufgabe 1184 of Elemente der Mathematik 57(3) (2002), how to transform the altar of Delos, presumably a cuboid with edge proportions 2:1:1, into a cube by cutting and reassembling. In this process only finitely many pieces with finitely many vertices, ie. polyhedra, should be used.
The question of equidecomposable (or scissors equivalent) polyhedra has a long history: Already the ancient Greek determined areas of trianlge and parallelograms by this mean. And despite nobody wrote it down in that age: they could have -with the methods known to Euclid- proved the theorem of Wallace, Bolyai and Gerwien, that any two polygons (plane polyhedra) of same area are equidecomposable. Here, we consider the corresponding problem in space. Gauß wondered 1844 in two letters to Gerling, that the known proofs that two tetrahedra with same bases and same height have the same volume, needed dissections into infinitely many pieces. Hilbert picked this up 1900 at the second International Congress of Mathematicians in Paris in his third problem and asked for two not equidecomposable tetrahedra with same bases and heiight. Only a few month later Max Dehn (1900) was able to settle the question by defining a dissection invariant, that gave different values for cube and tetrahedron.
In this article we describe a solution of Ernst Specker's exercise and discuss the background.
Zusammenfasssung
Ernst Specker fragte in Aufgabe 1184 der Elemente der Mathematik 57(3) (2002), wie man den Altar von Delos, vorgeblich ein Quader mit Kantenverhältnis 2:1:1, in einen Würfel verwandeln kann durch Zerschneiden und Wiederzusammensetzen. Dabei sollen nur endlich viele Teile mit jeweils endlich vielen Ecken, also Polyeder, verwendet werden.
Die Frage nach zerlegungsgleichen Polyedern reicht weit zurück: Schon die Griechen haben Flächen von Dreiecken und Parallelogrammen auf diese Weise bestimmt. Und auch wenn es damals niemand aufgeschrieben hat: sie hätten -mit Euklids Methoden- ohne Weiteres zeigen können, dass je zwei Polygone (ebene Polyeder) gleicher Fläche zerlegungsgleich sind. Hier geht es um dasselbe Problem im Raum. Gauß wunderte sich 1844 in zwei Briefen an Gerling, dass man beim Beweis der Volumengleichheit zweier Tetraeder mit gleicher Grundfläche und Höhe Zerlegungen in unendlich viele Teile benötigt. Hilbert griff dies 1900 auf dem zweiten Internationalen Mathematikerkongress in Paris in seinem dritten Problem auf und fragte nach zwei nicht zerlegungsgleichen Tetraedern gleicher Grundfläche und Höhe. Schon wenige Monate später konnte Max Dehn (1901) die Frage tatsächlich entscheiden, indem er eine Invariante angab, die für Würfel und Tetraeder unterschiedliche Werte liefert.
Wir beschreiben in diesem Artikel eine Lösung des zweiten Autors zu Ernst Speckers Aufgabe und erläutern die Hintergründe.
Material
- A film of the 8 piece solution: MapleWorkSheet, Animated-GIF.
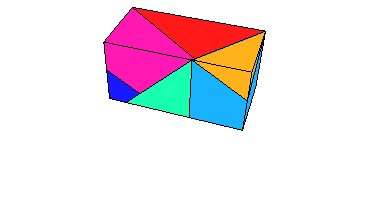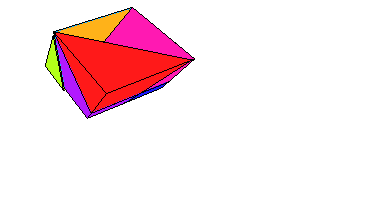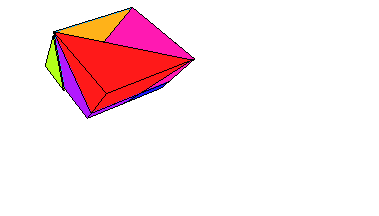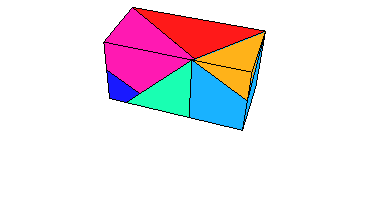
- A second film of the 8 piece solution with linear movements: MapleWorkSheet, Animated-GIF.
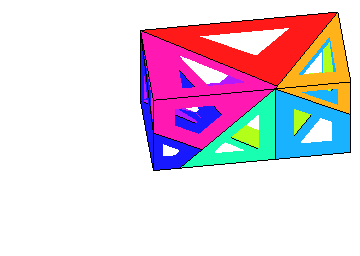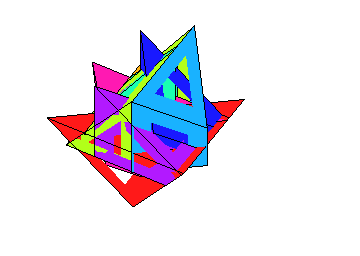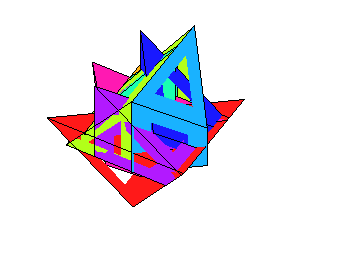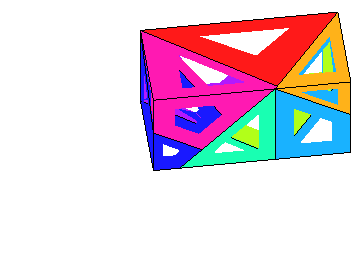
- A film of the 7 piece solution: MapleWorkSheet, Animated-GIF.
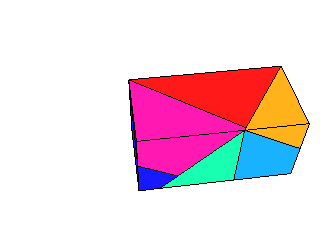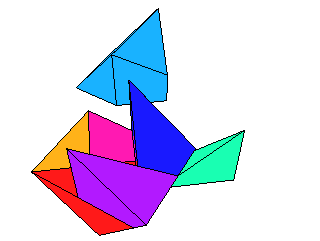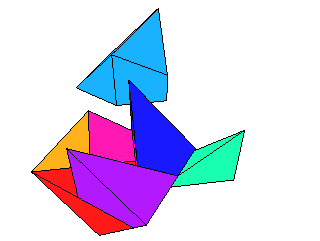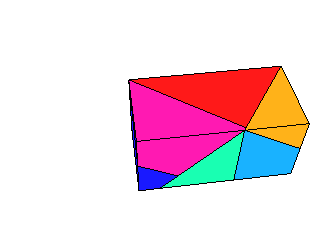
- The complete Maple 8 worksheet with the development of the solution: MapleWorkSheet, PDF.
- Nets: Build your own seven pieces!
The resolution of all images is the same and chosen such that printing with 144dpi gives small but fine modells. The edge length of the cube is then about 5cm. If you like it a little larger, print with 100dpi or even 72dpi. In the last case, however, the images do not fit on a A4 or letter paper and you have to print them in several chunks. Finally cut out the patterns by adding a suitable margins for gluing!





